非平稳序列的主成分分析

作者和客座文章作者：Eren Ocakverdi

这篇博客文章旨在介绍一个新的插件（即HXPRINCOMP），该插件实现了 Hamilton 和 Xi (2022) 开发的程序。

Hamilton 和 Xi（2022）在论文中提出了一种新颖的方法，其目标是提取所研究的每个序列的周期性成分背后的共同因素。他们认为，关注时间序列的周期性成分具有实际优势。也就是说，可以使用 OLS 回归来一致地估计它，同时对基础序列的平稳性保持不可知性。

该过程首先估计每个变量的以下 OLS 回归：

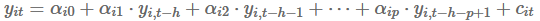
这里，（h=8）和（p=4）对于季度数据和（h=24）和（p=12）\每月数据。作者假设真正的周期性成分，

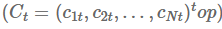
以因子结构为特征形式：

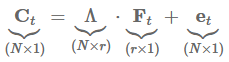
作者还表明，即使周期性成分未被观察到并因此被估计，在某些条件下仍然可以一致地估计真实因素。

作为第一个例子，作者将他们的方法应用于不同期限的国债收益率（见图 1）。

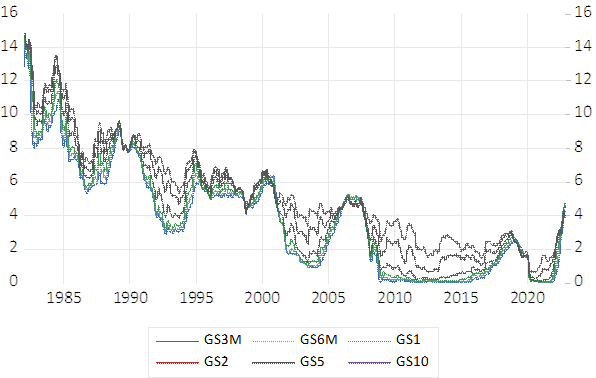
原始收益率数据的下降趋势很明显，但作者不喜欢应用任何变换来使该序列平稳。要在产量数据上运行该过程，我们可以使用该插件（参见图 2）。

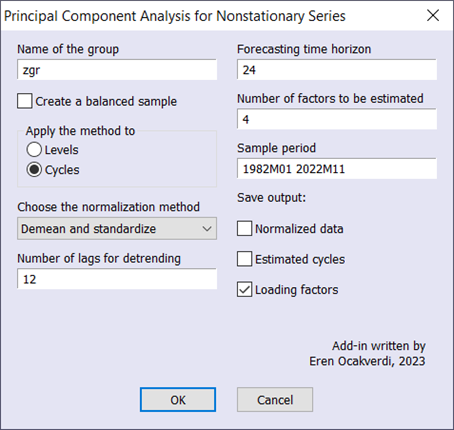
输入参数设置为与原始研究相匹配。提取了四个主要成分。然而，负载因子是本次特定练习的主要关注点，因为它们是总结收益率曲线动态的关键参数（见图 3）。

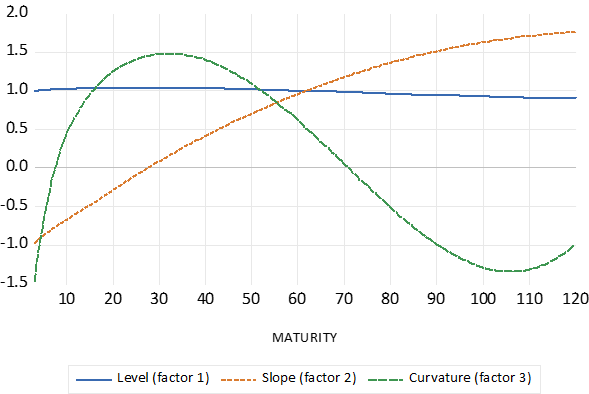
与第一个因素相关的收益率系数称为水平因素，并且对于所有期限都或多或少相同。第二个因素的负载称为斜率，对于长期利率为正，对于短期利率为负。第三个因素称为曲率，对于期限很短或很长的债券具有负权重。

当对大型宏观经济数据集使用主成分分析时，可能需要对每个变量进行变换以确保平稳性。由于它是单独完成的，因此这可能是一项乏味的任务。提取序列的循环分量通过设计解决了这个问题。

作为第二个例子，作者将他们的方法应用于大型宏观经济数据集（2022-4 年份的 FRED-MD 数据库），其中涵盖 127 个变量。要对宏观经济数据运行该过程，我们可以再次使用该加载项（参见图 4）。

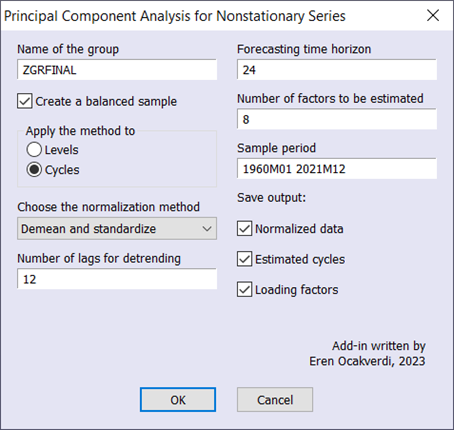
为了处理数据集中的缺失值，使用平衡样本。提取了八个主要成分，前两个成分如下图 5 所示。

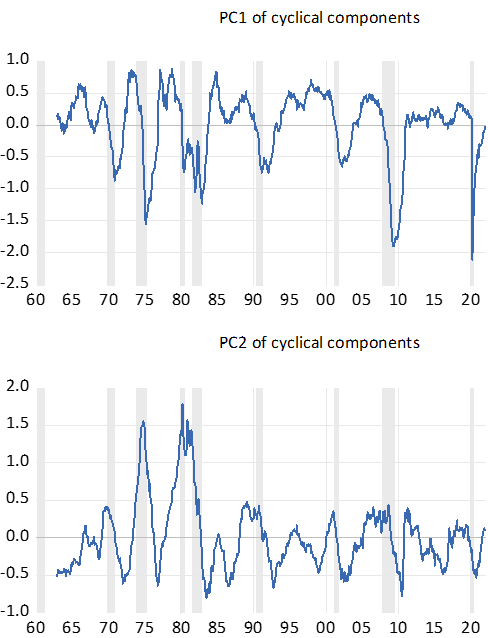
作者认为，他们的系列不仅正确地总结了早期的周期性变动，而且特别是在 2020 年期间。他们发现，虽然第一个因素反映了实际经济状况，但第二个因素主要与名义价格和利率有关。请注意，该过程不需要对序列进行任何平稳性校正或对异常值进行特殊处理！