通过卡尔曼滤波估计局部线性趋势

作者和客座文章作者：Eren Ocakverdi

这篇博文旨在介绍一个新的插件（即 LOCALLINEAR），它通过卡尔曼滤波器估计局部线性趋势。

滤波趋势组件是总结时间序列数据的一种有用方法，因为它允许人们捕获并关注真正重要的重要特征。但是，滤波方法可能会导致信息丢失，因此需要付出代价。尽管如此，线性状态空间模型（LSSM）提供了一种实用的方法来提取观察到的变量的未观察到的趋势分量。

Add-in 实现以下框架：

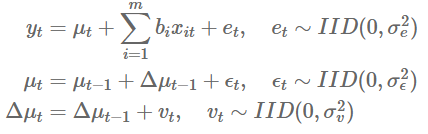
上面的模型非常灵活，这使得在实践中很难区分未观察到的趋势值和实际水平。在这种情况下，将趋势方程的方差限制为零（即）可能有助于获得平滑的随机趋势。也可以施加外生惩罚参数（即）并控制趋势的平滑度（即），如 Hodrick-Prescott 滤波器的意义。

任何类型的解释变量或干预效应都可以通过信号方程中的回归器添加到模型中。

高频金融变量通常是由于多种原因而产生的噪声，其中大多数即使在事后也无法控制或识别。过滤掉因市场条件逐期变化而自然产生的噪音成分，可以为我们提供潜在趋势的清晰图景，而不会损失太多关键信息。在本练习中，使用了土耳其的每周信用卡支出数据（见图 1）。

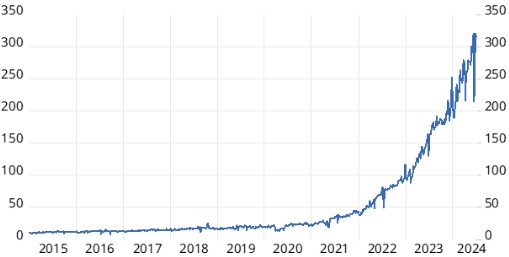
信用卡支出数据在各个级别中看起来并不平滑，但当我们查看每周变化时，它变得更加不稳定（见图 2）。

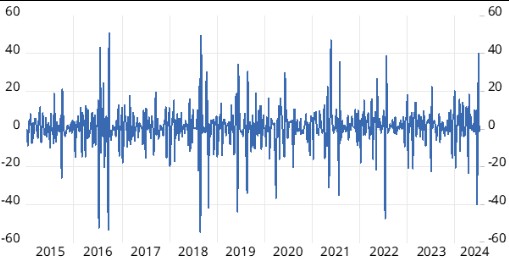
数据中频繁而严重的峰值使得难以读取潜在的动态。随机趋势估计可能有助于过滤掉数据中的此类波动。

要估计局部线性趋势模型，我们可以使用插件（参见图 3）。

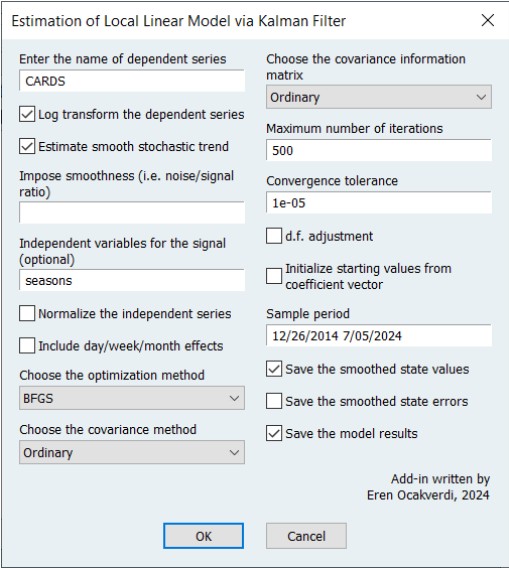
采用对数有助于减轻此类名义变量中通常存在的尺度效应。平滑随机趋势的估计也可能有助于进一步降低潜在分量中的噪声。最后，我们可能需要考虑季节性，看看支出模式是否会随着日历月的变化而变化（见图 4）。

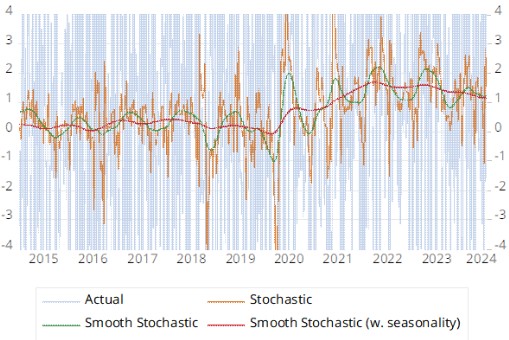
在过滤掉噪音并控制季节性影响后，信用卡支出的势头损失变得更加明显。