单变量 GARCH 模型的广义自回归评分（GAS）方法

作者和客座博文作者：Eren Ocakverdi

这篇博文旨在介绍一个新的插件（即 GASMODELU），用于估计广义自回归评分（GAS）框架内选定的单变量 GARCH 模型。

Creal 等人。al. （2013）提出了一类观察驱动的时间序列模型，称为广义自回归评分（GAS）模型。在对参数中的时间变化进行建模时，观测驱动方法允许使用滞后因变量或同时期和滞后外生变量。由于参数随时间推移的更新机制基于似然函数的比例分数，因此 GAS 方法包括其他知名模型，例如 GARCH。

让我们表示作为感兴趣的因变量，作为时变参数向量，将作为静态参数的向量。那么 GAS 框架可以概述如下：

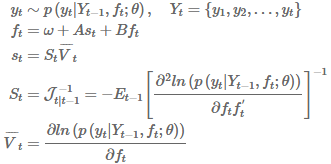
该方法基于给定参数的观测密度。当观测已实现，时变到下一个期间会相应地更新。缩放矩阵通常定义为得分方差的函数。这样做会得出 GARCH 模型的一个特例：

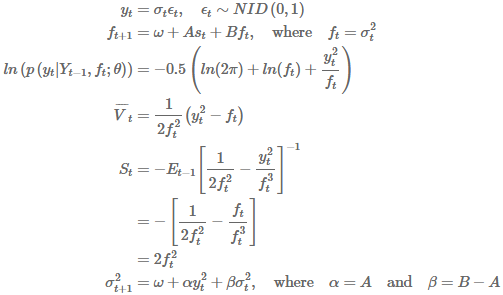
虽然最终结果对于高斯分布而言会变成标准的 GARCH(1,1) 模型，但对于厚尾分布而言并非如此。例如，具有 Student’s-t 误差的模型的 GAS 更新机制与 GARCH 模型非常不同：

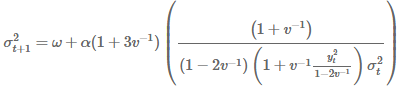
请注意，如果取非常大的正值/负值，它会相应地被拉低，因此方差的增加仍然小于具有 Student’s-t 误差的常规 GARCH。这一结果也与金融市场的典型事实相一致，其中观察到的突然跳跃对未来波动的影响小于标准模型的预测。

土耳其外汇市场为探索货币冲击对波动性动态的影响提供了一个有用的实验室（usdtry.wf1）。下面的图 1 显示了每日回报的平方值，在 2015-2023 年的样本期间，至少可以目视识别出三次严重冲击（gasmodelu_example.prg）。

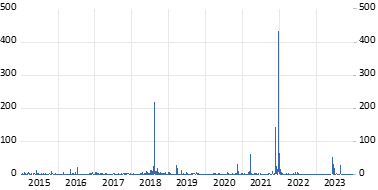
首先，我们首先估计三个对创新具有不同分布假设的 GARCH 模型，然后使用插件估计 GAS 对应项以进行比较。从方程对象调用插件将提示 GUI（参见图 2）。

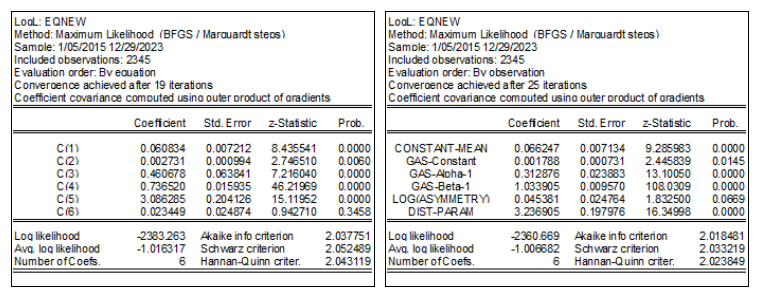
除了由于优化设置而产生的细微差异外，高斯假设的结果几乎相同（参见图 3）。这是意料之中的，因为从数学角度来看，GARCH 方程和 GAS 方程的系数基本相同。请注意，GAS 方程的 Beta 系数等于（并且应该）等于 GARCH 方差方程的自回归系数之和。

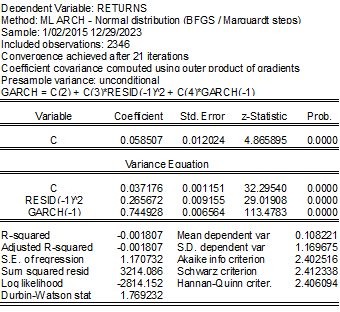
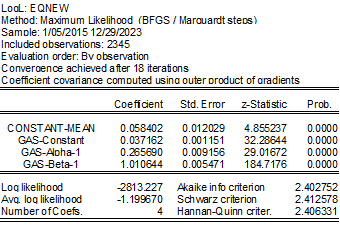
在高斯分布的情况下，估计的条件方差和得分值彼此无法区分（见图 4）。

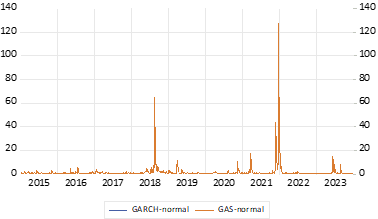
从这个意义上说，其他分布（即厚尾分布）的估计结果并不相同，也不具有直接可比性（见图 5 和图 6）。

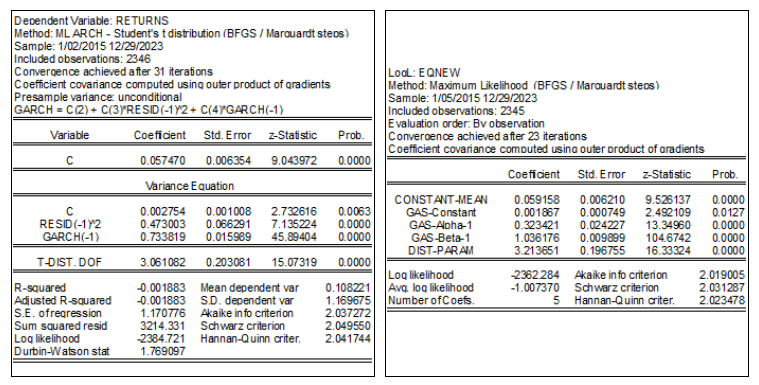
请注意，对于 Skewed GARCH 结果，您需要使用插件 SKEWEDUGARCH 来获得结果

图 7 和图 8 描述了学生 t 分布和偏斜版本学生 t 分布的估计条件方差和分数的比较。

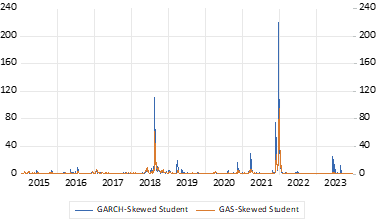
GAS 模型减轻了回报大幅变化的影响，因为它们通常是一次性事件，并且与较小的冲击相比，对未来波动性的影响相对较小。这主要是由于市场对新信息的弹性和适应性。