第 2 部分：强大的分析工具 - EViews 14

与其他计量经济学软件相比，大多数用户没有理由学习复杂的命令语言。EViews 的内置程序只需点击鼠标即可，并提供实际计量经济学和预测工作中最常用的工具。

基本统计分析

EViews 支持范围广泛基本统计分析，包括简单的描述性统计到参数和非参数假设检验。

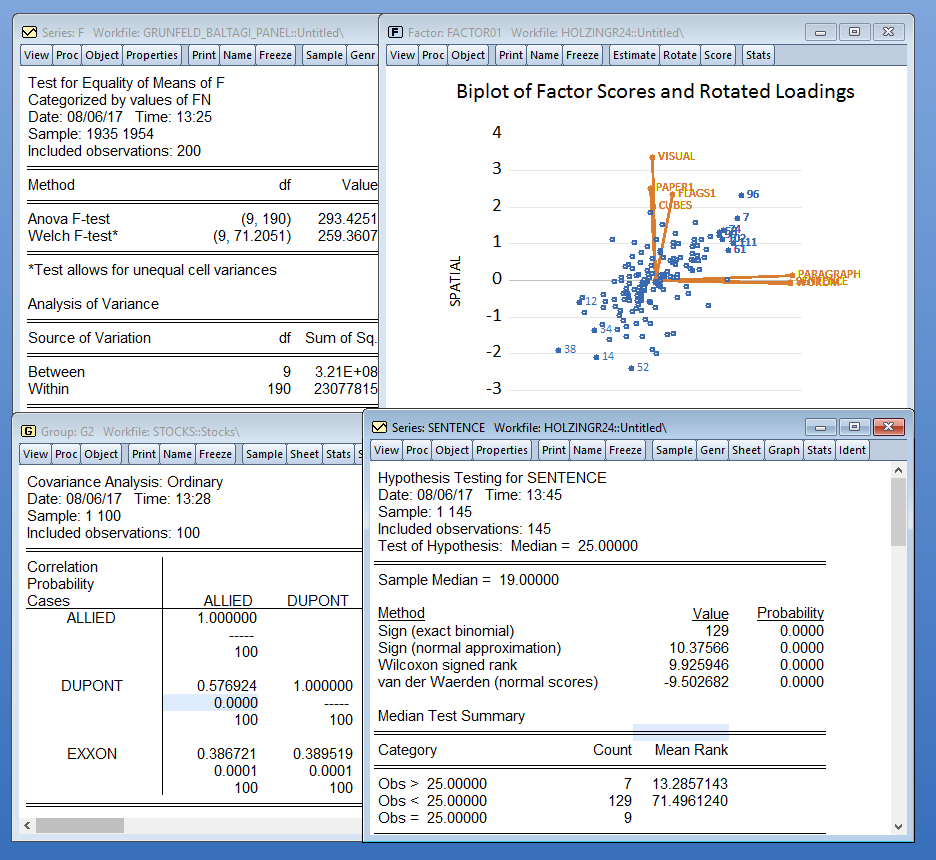
基本的描述性统计可以快速轻松地进行通过基于一个或多个变量的分类，或通过面板或合并数据中的横截面或周期。均值、中位数和可以进行方差测试，包括针对特定值进行测试，测试序列之间的相等性，或按其他变量（允许您执行单因素方差分析）。协方差和因子的工具分析允许您检查变量之间的关系。

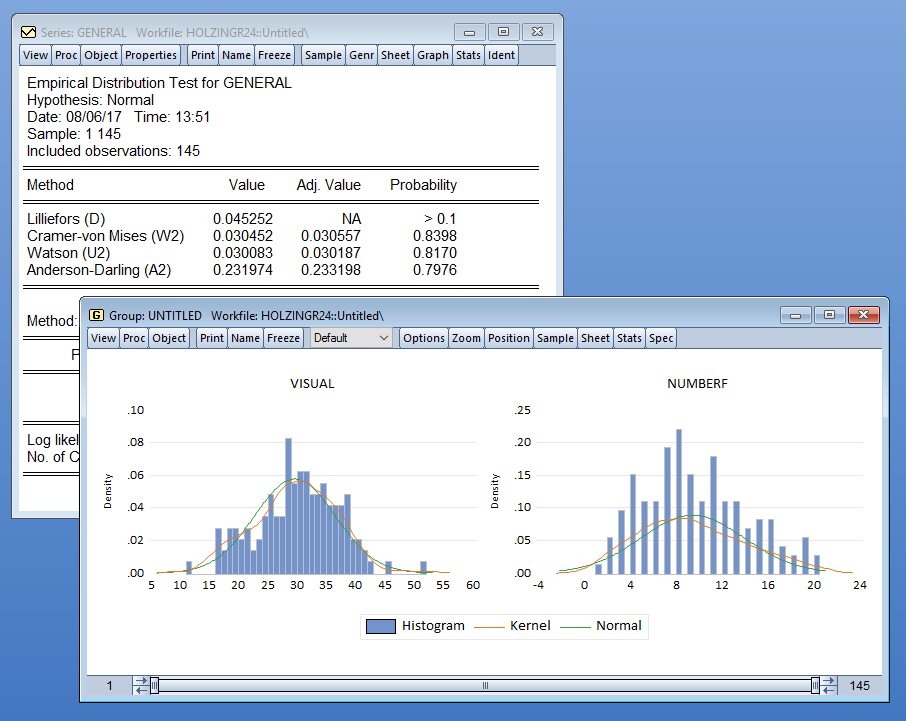
您可以使用以下方法可视化数据的分布直方图、理论分布、核密度或累积分布，幸存者图和分位数图。QQ图（分位数-分位数图）可用于比较一对序列的分布，或单个序列相对于各种理论分布。

您甚至可以表演 Kolmogorov-Smirnov、Liliefors、Cramer von Mises 和 Anderson-Darling 检验以查看序列是否呈正态分布，或者它是否来自另一个分布，例如指数、极值、 logistic、卡方分布、Weibull 或 gamma 分布。

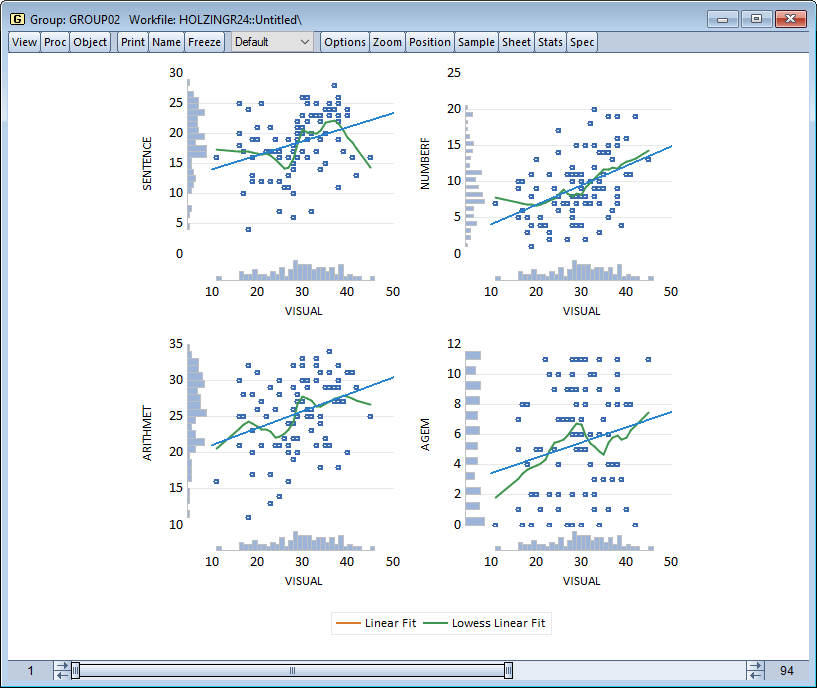
EViews 还使用普通回归、变换回归、核回归和最近邻回归。

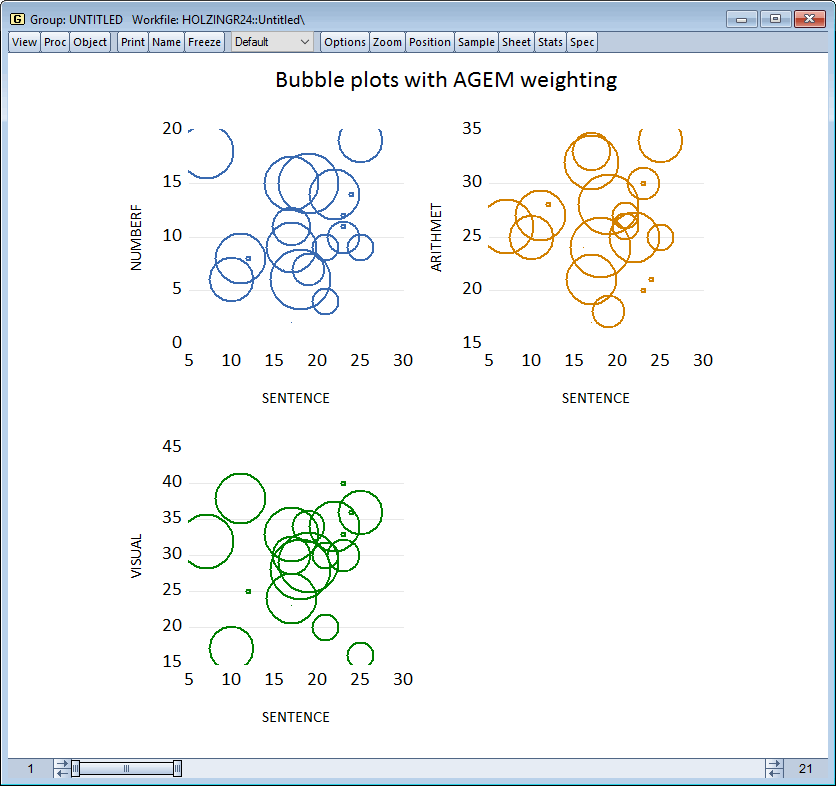
气泡图允许您使用第三个序列来确定散点图中点的大小。

时序统计和工具

探索时间序列使用从简单的自相关图到频率的工具对数据进行属性分析筛选到 Q 统计量以对根测试进行单元分析。

EViews 提供自相关和偏自相关函数、Q 统计量和互相关函数，以及单位根检验（ADF、 Phillips-Perron、KPSS、DFGLS、ERS 或 Ng-Perron 用于单个时间序列和 Levin-Lin-Chu、Breitung、Im-Pesaran-Shin、Fisher 或 Hadri 用于面板数据，以及断点单位根和季节性单位根检验）、协整检验（Johansen with MacKinnon-Haug-Michelis 临界值和 p 值为普通值数据，以及 Pedroni、Kao 或 Fisher 的面板数据）、因果关系和独立性检验。

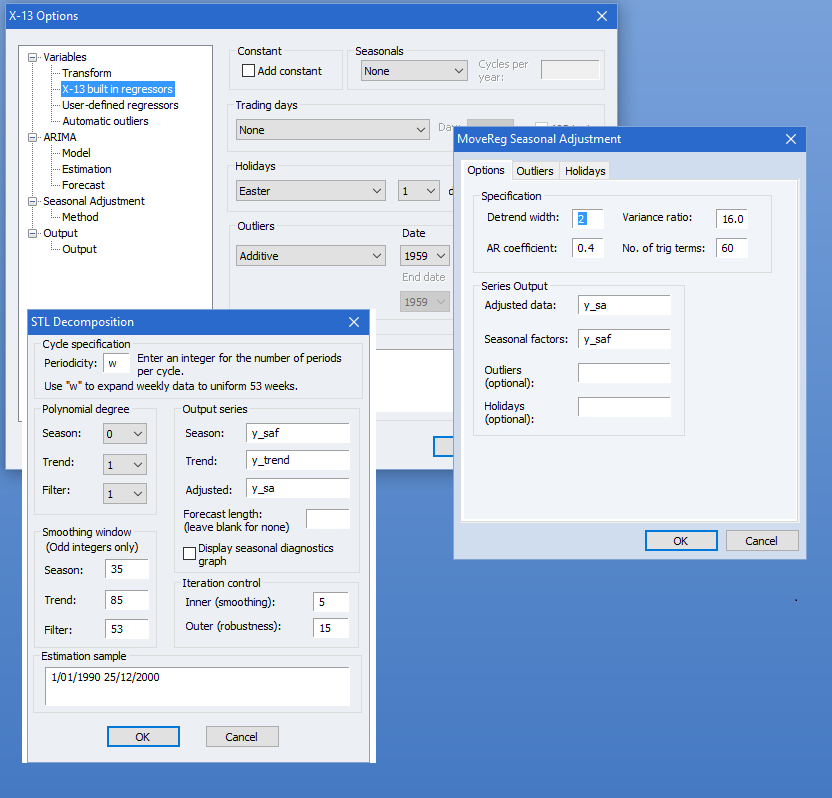
EViews 还提供易于使用的前端支持美国人口普查局的 X-13 季节性调整计划，以及 MoveReg 获取美国劳工统计局的每周数据。 STL分解为任何频率数据提供季节性调整，并且还使用加法和乘法差分方法进行简单的季节性调整在 EViews 中受支持。

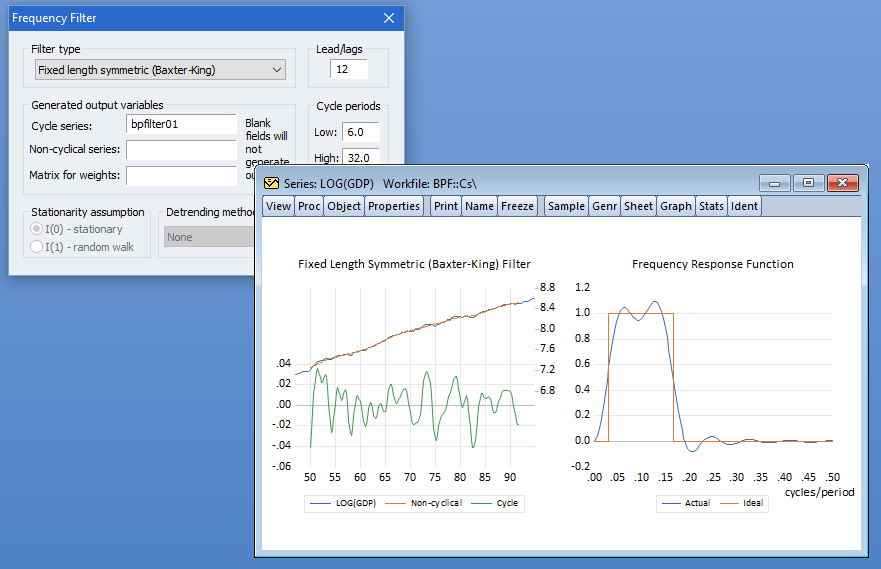
您甚至可以使用 EViews 来计算趋势和使用 Hodrick-Prescott、Baxter-King、 Christiano-Fitzgerald 固定长度和 Christiano-Fitzgerald 不对称全样本带通（频率）滤波器。

面板和汇总数据统计和工具

EViews 具有多种工具，旨在促进面板或池/时间序列交叉的工作部分数据。定义面板结构，对面板数量几乎没有限制横截面或组，或组中的周期数或观测值数。日期或未注明日期、平衡或不平衡以及规则或不规则频率面板数据集是所有这些都在 EViews 框架内自然处理。

数据结构工具促进数据从堆叠（面板）到非堆叠（池）的转换格式，然后再返回。智能链接、自动序列和数据提取工具允许您轻松对数据进行切片、匹配、合并、频率转换和汇总。

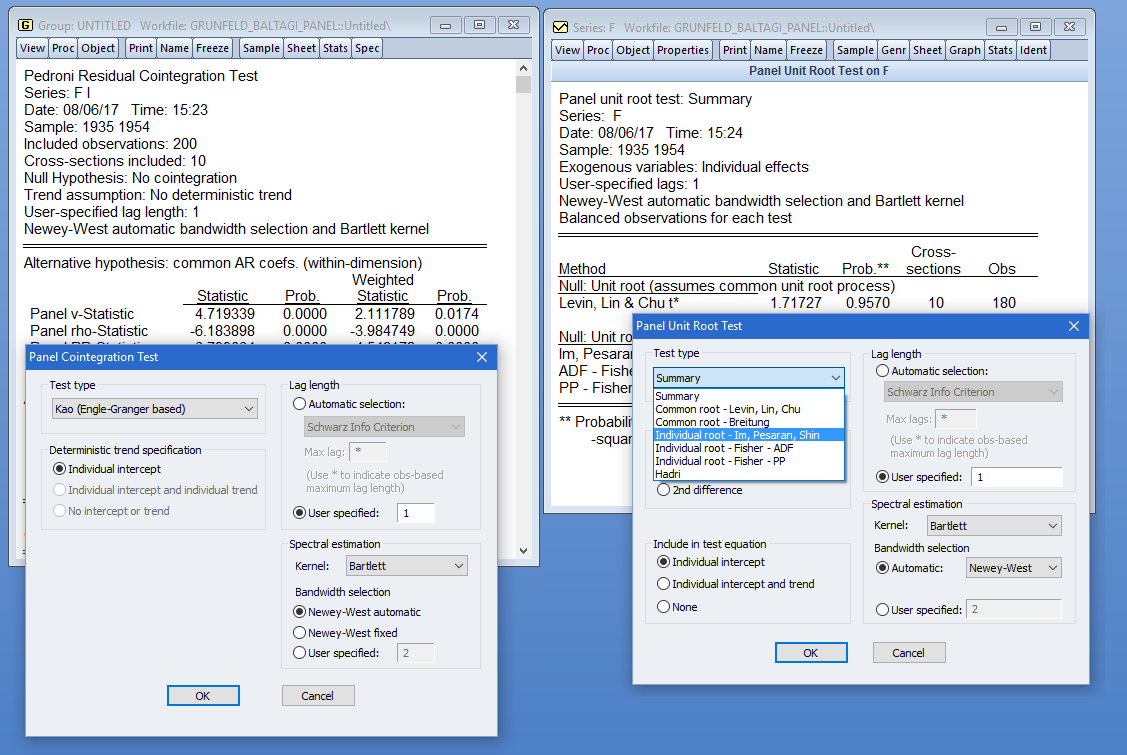
支持基本的纵向数据分析范围，包括方便的按组和按周期统计、测试和图形，到复杂的面板单元根（Levin-Lin-Chu、 Breitung、Im-Pesaran-Shin 或 Fisher）和协整诊断（Pedroni （2004）、Pedroni （1999）和 Kao，或 Fisher 型测试）。

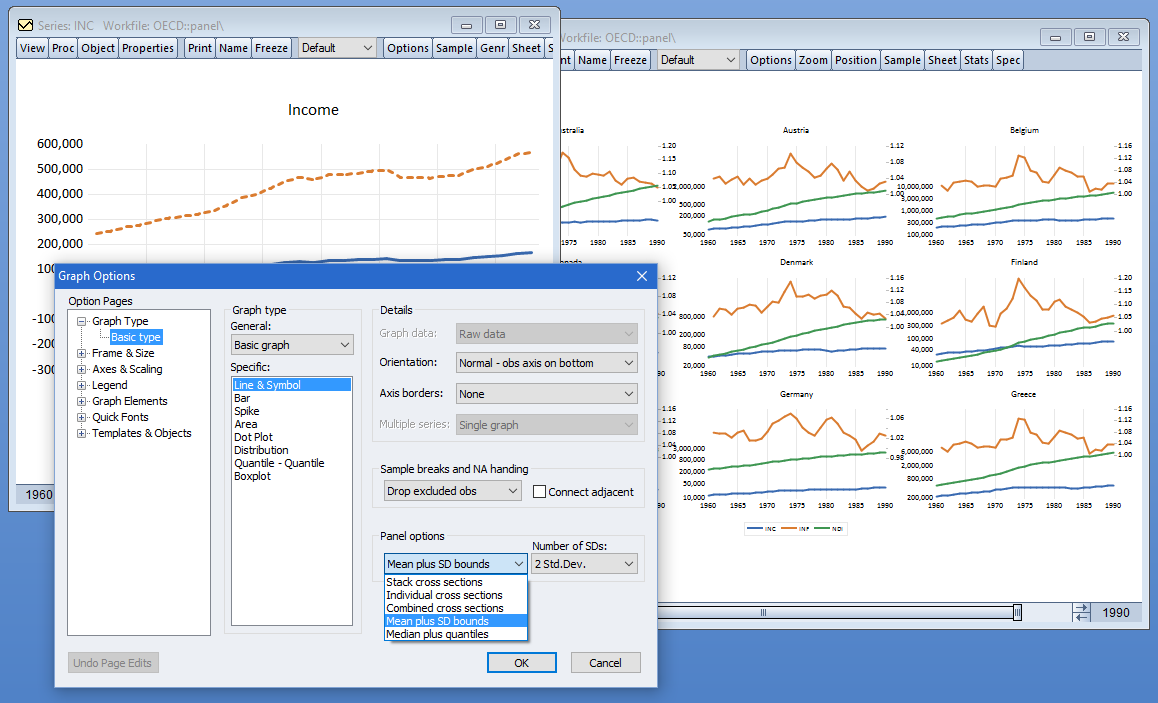
用于显示面板数据图的专用工具允许您查看堆叠的、单独的、或摘要显示。在单个图形框架中或单个框架。或显示所获取的面板数据的汇总统计信息横截面，带有平均值（或中位数）和标准差（或分位数）带。

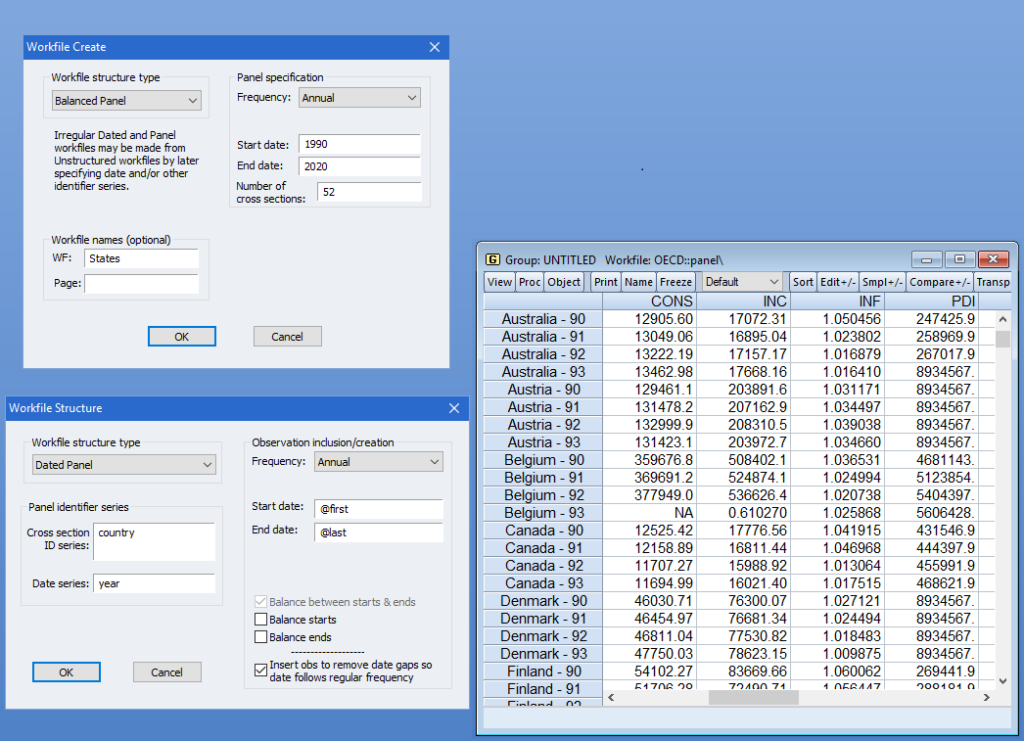
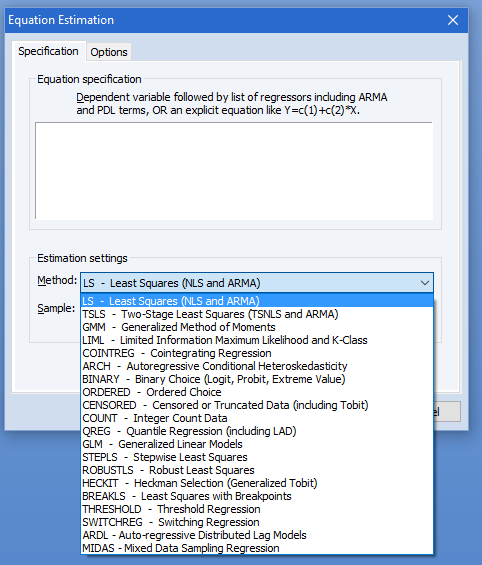
单方程估计

EViews 允许您从一整套基本的单方程估计器中进行选择，包括：普通和非线性最小二乘法（多元回归）、加权最小二乘法、两阶段最小值平方（工具变量）、分位数回归（包括最小绝对偏差估计）和逐步线性回归。加权所有这些技术都可以进行估计。规格可能包括任意数量的自变量上的多项式滞后结构。

对于时间序列分析，EViews 估计 ARMA 和 ARMAX 模型，以及各种 ARCH 规范。可以使用状态空间对象来估计结构时间序列模型。

除了这些基本的估算器之外，EViews 还支持各种高级模型的估计和诊断。

广义矩量法（GMM）

EViews 支持两者的 GMM 估计横截面和时间序列数据（单方程和多方程）。加权选项包括用于横截面数据的怀特协方差矩阵和各种 HAC 协方差时间序列数据的矩阵。HAC 选项包括预白化、各种内核以及固定、Andrews 或 Newey-West 带选择方法。您可以使用迭代过程或持续更新过程来估计 GMM 方程。GMM方程的估计后诊断，包括弱仪器统计数据，也可用。

ARCH

如果序列的方差随时间波动， EViews 可以使用各种自回归来估计方差的路径条件异方差性 ARCH）模型。EViews 处理 GARCH（p，q）、EGARCH（p，q）、 TARCH（p，q）、PARCH（p，q）和组件 GARCH 规范，并提供最大似然对遵循正态的误差的估计，学生的 t 或广义误差分布。ARCH 的平均方程模型可能包括 ARCH 和 ARMA 项，均值方程和方差方程都允许外生变量。

有限的因变量

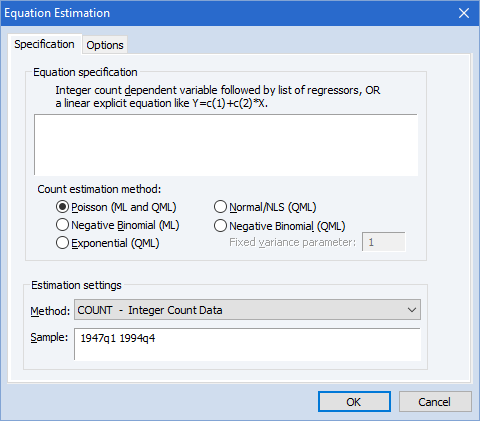
EViews 还支持对一系列有限因变量模型的估计。二元模型、有序模型、删失模型和截断模型可以估计可能性基于正态误差、逻辑误差和极值误差的函数。计数模型可以使用泊松、负二项式和准最大似然（QML）规范。Heckman Selection模型提供两步估计或MLE估计。EViews（可选）报告广义线性模型或QML标准误差。

其他估算器

EViews 还提供鲁棒最小二乘法、弹性网络、岭回归、LASSO、函数系数、逐步、MIDAS（混合频率）和阈值模型的估计。

面板和合并时间序列 – 横截面

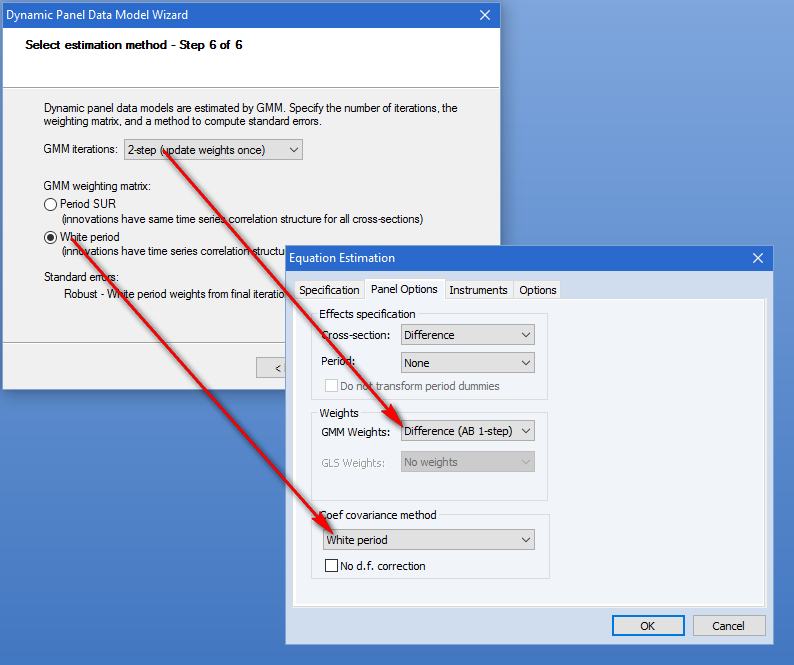
EViews 提供各种面板和汇总数据估算方法。除了普通线性和非线性最小二乘法外，方程估计方法包括 2SLS/IV 和广义 2SLS/IV，以及可用于估计的 GMM 复杂的动态面板数据规范（包括 Anderson-Hsiao 和 Arellano-Bond 估算器的类型）。

大多数方法都允许时间和横截面固定和随机效果规格。对于随机效应模型，二次无偏分量方差的估计器包括 Swamy-Arora、Wallace-Hussain 和 Wansbeek-Kapteyn。

还支持 AR 规范（任何效果都是变换后定义）、加权最小二乘法和看似不相关的回归。在池中，特定变量（包括 AR 项）的系数可以限制为相同，或允许在横截面之间有所不同。

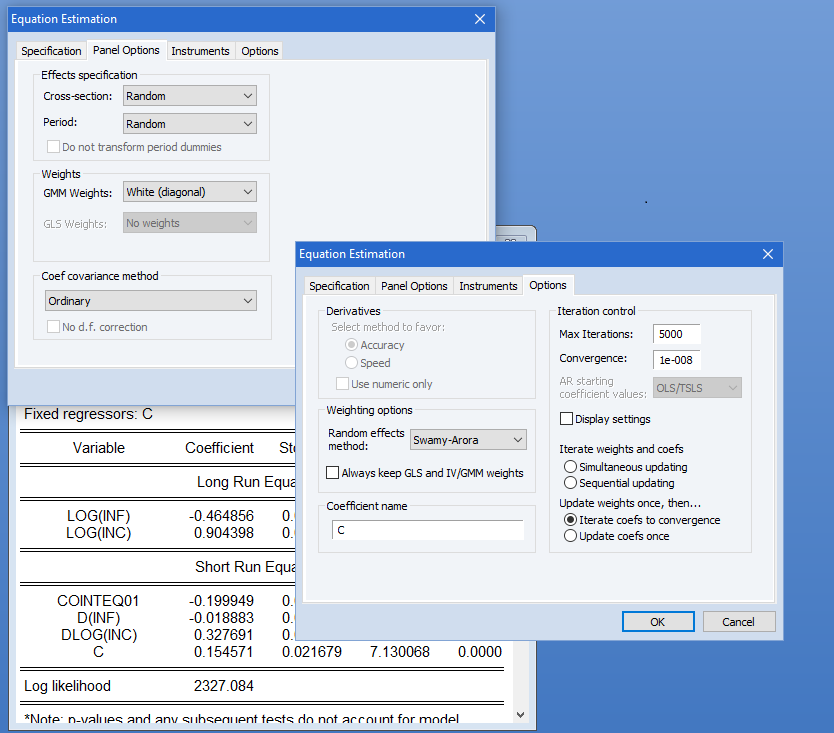
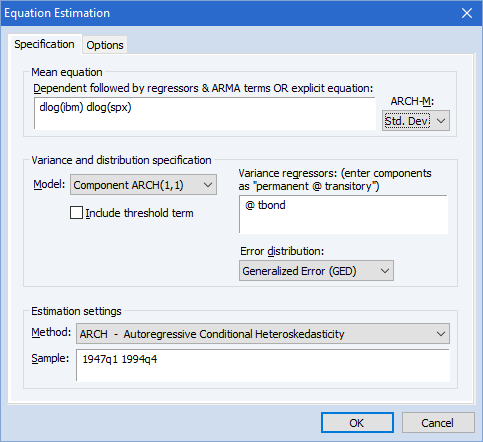
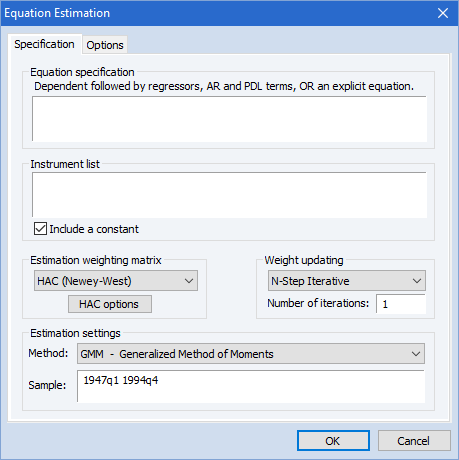
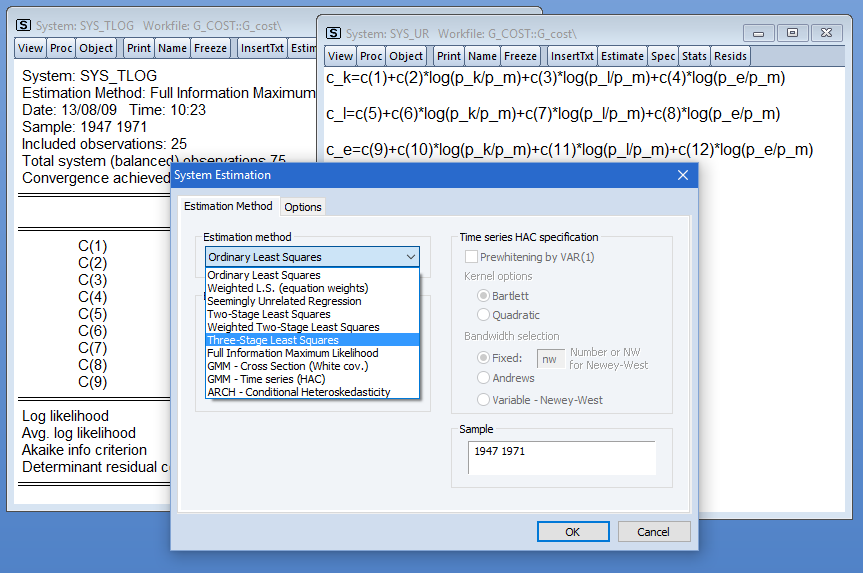
系统估计

EViews 还提供强大的分析工具方程组。您可以使用 EViews 进行估算 OLS的线性和非线性方程组，两阶段最小二乘法，看似无关的回归、三阶段最小二乘法、GMM 和 FIML。系统可以包含交叉方程限制，在大多数情况下，包含任意阶次的自回归误差。

向量自回归/纠错模型

向量自回归、贝叶斯 VAR、混合频率 VAR、马尔可夫切换 VAR 和向量纠错模型 EViews 可以很容易地估计。估计后，您可以检查脉冲响应 VAR 或 VEC 的函数和方差分解。VAR 脉冲响应函数分解具有通过分析或 Monte 计算的标准误差 Carlo 方法（解析方法不可用于分解），并且可以显示在各种图形和表格格式。

您可以对协整关系和/或调整系数。EViews 的 VAR 还允许您通过施加短期（Sims 1986）或长期来估计结构因式分解（VAR）（Blanchard 和 Quah 1989）限制，或两者兼而有之。可以使用以下方法测试过度识别限制 EViews 报告的 LR 统计数据。

VAR 支持多种视图，允许您检查估计规格的结构。只需点击几下鼠标，即可显示特征 AR 多项式的反根，执行格兰杰因果关系和联合滞后排除测试，评估各种滞后长度标准，查看相关图和自相关，或执行各种基于多变量残差的诊断。

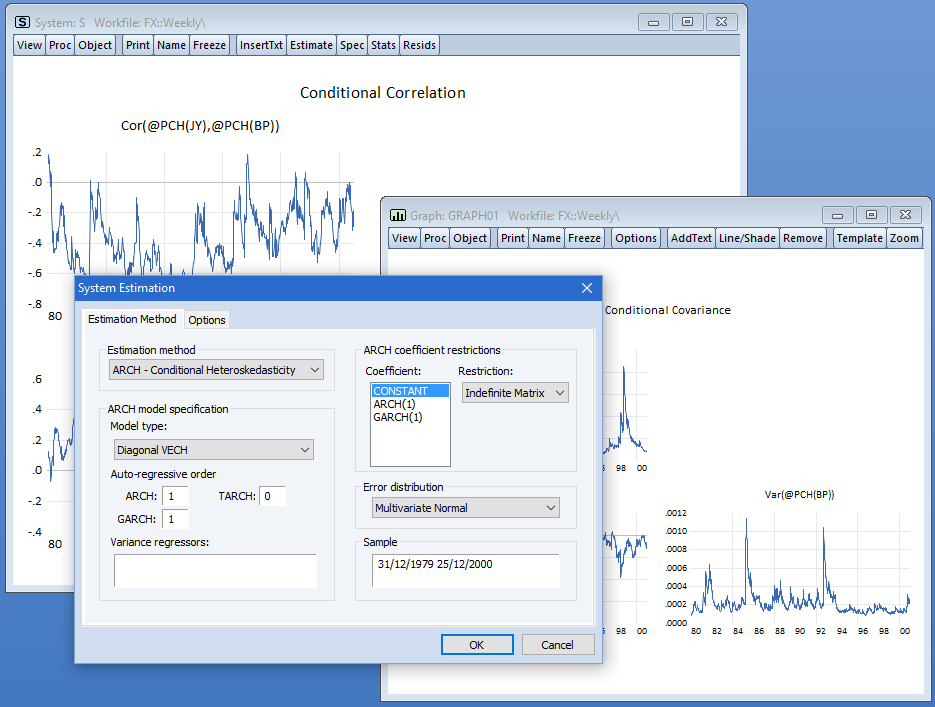
多变量 ARCH

多变量 ARCH 可用于模拟时变多个时间序列的方差和协方差。许多流行的 ARCH 型号，例如条件常相关（CCC）、对角线 VECH 和对角线 BEKK 是可用。均值方程和方差方程中允许使用外生变量;非线性和 AR 项可以包含在均值方程中。假定错误为分发为多变量 Normal 或 Student’s t。此外，还提供Bollerslev-Wooldridge稳健标准误差。一旦模型被估计，用户就可以很容易地生成样本内方差，表格或图形格式的协方差或相关性。

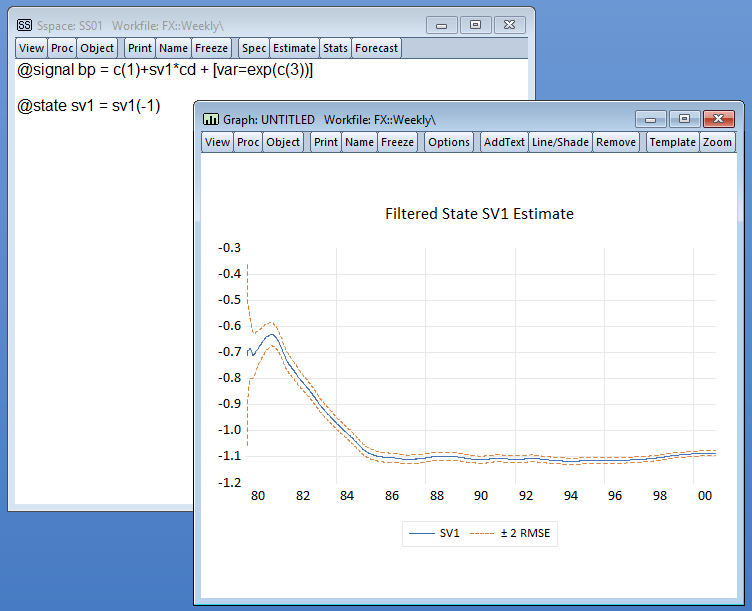
状态空间模型

状态空间对象允许估计各种各样的使用卡尔曼滤波的单方程和多方程动态时间序列模型算法。除此之外，您还可以使用状态空间对象来估计随机和时变系数模型和ML ARMA规范。

复杂的过程和视图使您可以访问强大的过滤和平滑工具，以便您可以提前一步查看或生成，过滤或平滑的信号、状态或错误。EViews 的内置预测程序此外，还提供易于使用的工具，用于使用提前 n 步或平滑值进行样品内和样品外预测。

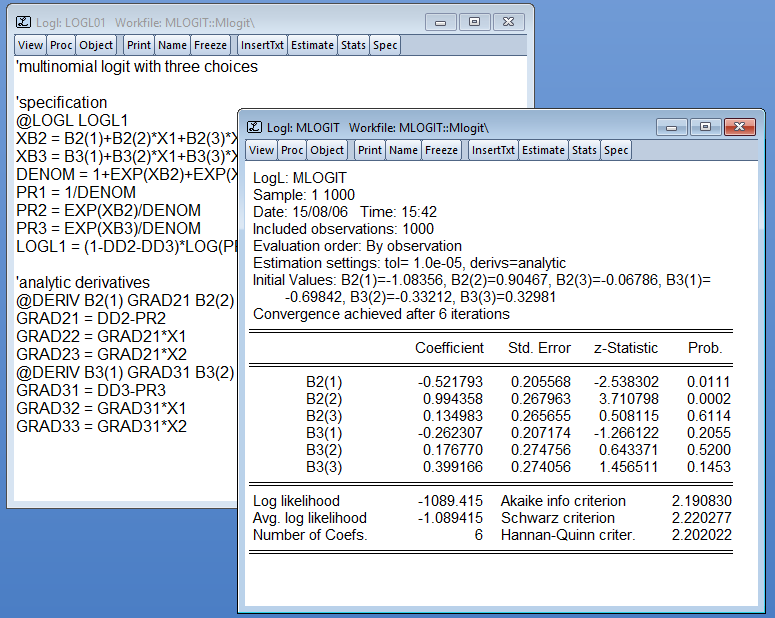
用户指定的最大似然法

对于自定义分析，EViews 易于使用的似然对象允许估计用户指定的最大似然模型。您只需提供标准 EViews 表达式，用于描述每个 EViews 的对数似然贡献观察样品，设置系数起始值，EViews 将完成剩下的工作。

<<直观、易于使用的界面 <—————–> 复杂的数据管理>>