大家好!今天我们要聊一个在数据分析领域非常有趣的话题——非平稳时间序列的主成分分析。这可不是普通的分析方法,而是由Hamilton和Xi在2022年提出的一种全新方法,并且专门开发了一个HXPRINCOMP加插件来实现这个过程。这个方法在处理经济数据时特别有用,尤其是当我们面对那些复杂的、非平稳的时间序列数据时。下面,就让我们一起来详细了解一下这个方法吧!
一、引言
在他们的论文中,Hamilton和Xi提出了一种新颖的方法,目的是提取每个研究序列背后共同的因子。他们认为,专注于时间序列的循环成分具有实际优势,因为这些成分可以使用OLS回归一致地估计,同时不必关心底层序列的平稳性。
二、循环成分的主成分分析
这个过程从估计每个变量的OLS回归开始:
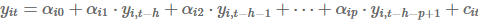
对于季度数据,h=8和 p=4;对于月度数据,h=24和 p=12
。作者假设真实的循环成分![]()
具有因子结构 r≪N:
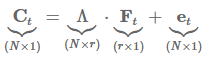
即使循环成分没有被观察到,而是被估计(![]() ),在一定条件下,真实的因子仍然可以被一致地估计。
),在一定条件下,真实的因子仍然可以被一致地估计。
三、应用于美国国债收益率
作为第一个例子,作者将他们的方法应用于不同期限的国债收益率(见图1)。

原始收益率数据的下降趋势很明显,但作者选择不对数据进行任何平稳化处理。为了在收益率数据上运行这个过程,我们可以使用加插件(见图2)。
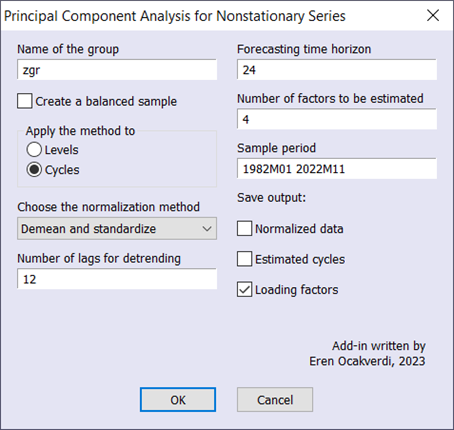
输入参数设置与原始研究相匹配。提取了四个主成分。然而,加载因子是这个练习中最重要的部分,因为它们是总结收益率曲线动态的关键参数(见图3)。
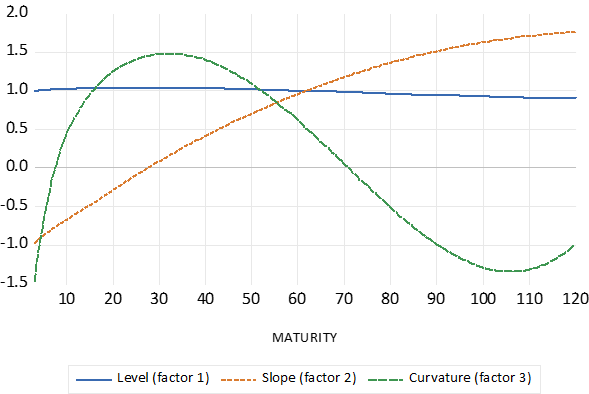
与第一个因子相关的收益率系数称为水平因子,对所有期限几乎相同。第二个因子的加载称为斜率,对长期利率为正,但对短期利率为负。第三个因子称为曲率,对期限非常短或非常长的债券有负权重。
四、应用于大型宏观经济数据集
在对大型宏观经济数据集进行主成分分析时,可能需要对每个变量进行转换以确保平稳性。由于这是单独完成的,可能是一项繁琐的任务。通过设计,提取序列的循环成分解决了这个问题。
作为第二个例子,作者将他们的方法应用于一个大型宏观经济数据集(FRED-MD数据库2022年4月的版本),该数据库涵盖了127个变量。为了在宏观经济数据上运行这个过程,我们再次可以使用加插件(见图4)。
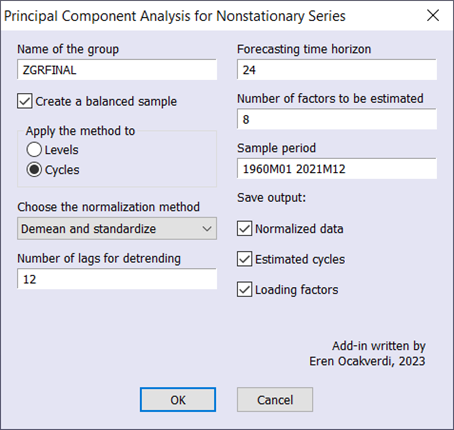
为了处理数据集中的缺失值,使用了平衡样本。提取了八个主成分,并在图5中展示了前两个。
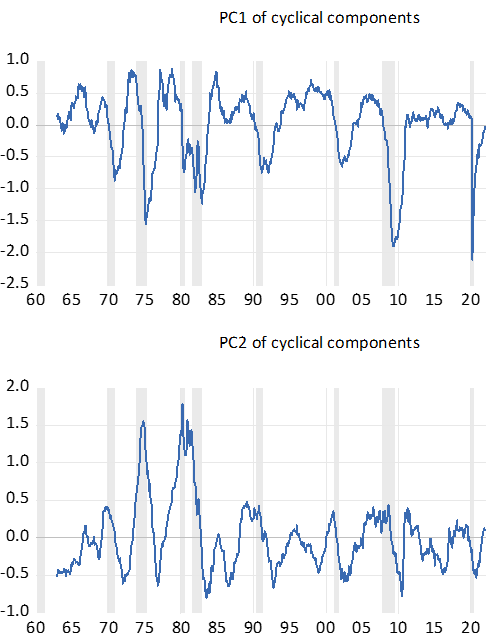
作者认为,他们的序列不仅正确总结了早期时期的循环运动,而且在2020年期间也是如此。他们发现,第一个因子捕捉了实际经济状况,而第二个因子主要与名义价格和利率相关。请注意,这个过程不需要对序列进行任何平稳性修正或对异常值进行特殊处理!
五、相关文件
六、参考文献
- Hamilton, J. D., and Xi, J. (2022), Principal Component Analysis for Nonstationary Series, Working Paper, UC San Diego.
希望这篇文章能帮助你更好地理解非平稳时间序列的主成分分析方法及其应用。如果你对这个话题感兴趣,不妨深入研究一下Hamilton和Xi的论文,或者尝试使用HXPRINCOMP加插件来分析你自己的数据。数据分析的世界充满了无限可能,让我们一起探索吧!
